Uncrossed Lines

Description

We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw connecting lines: a straight line connecting two numbers A[i] and B[j] such that:

• A[i] == B[j];
• The line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.

Return the maximum number of connecting lines we can draw in this way.

 

Example 1:

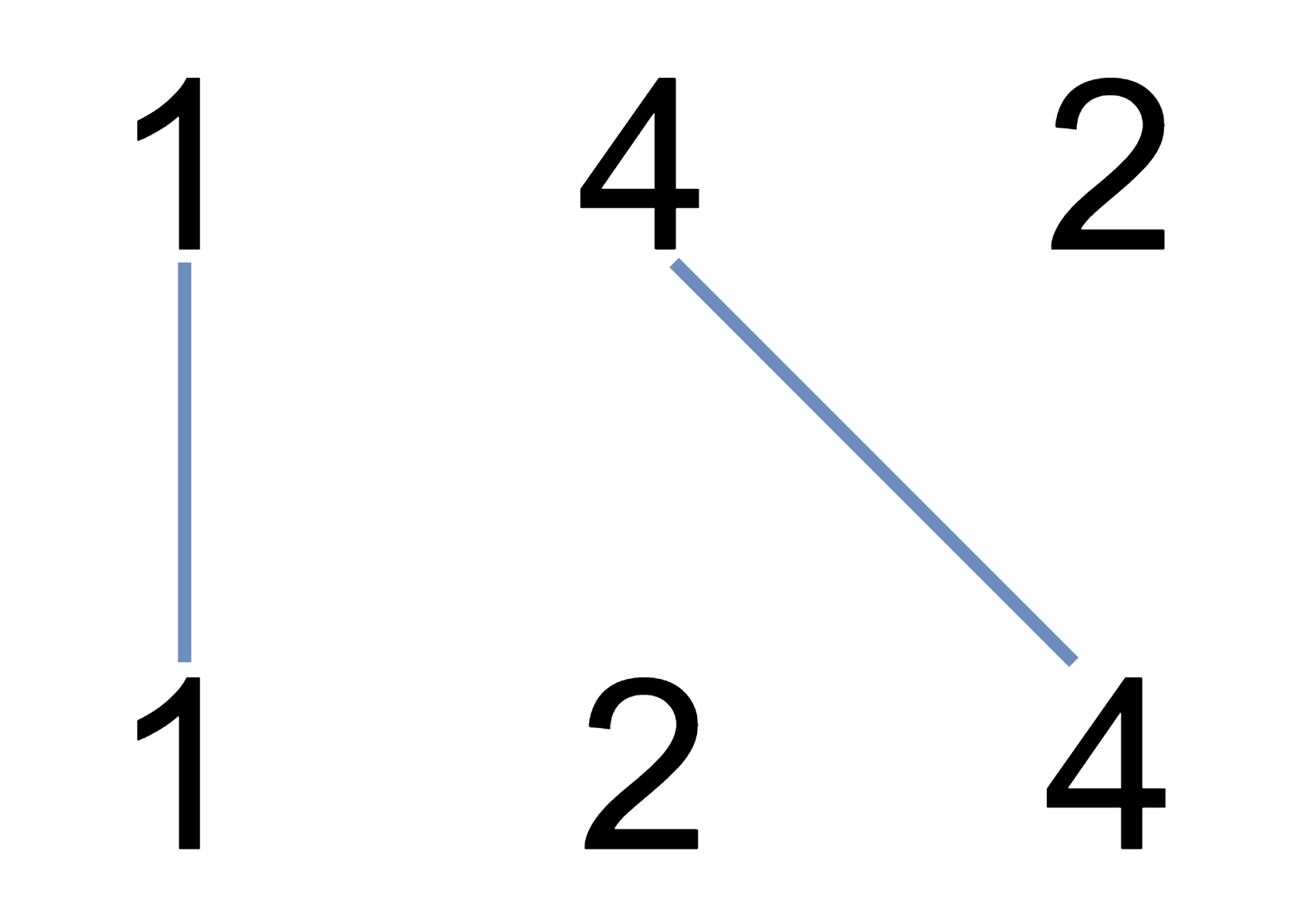
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Example 2:

Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Example 3:

Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

 

Note:

1. 1 <= A.length <= 500
2. 1 <= B.length <= 500
3. 1 <= A[i], B[i] <= 2000

Solution(javascript)

// DP O(m * n)
const maxUncrossedLines = function (A = [], B = []) {
  const map = {}
  const aux = (indexA, indexB) => {
    map[indexA] = map[indexA] || {}
    if (map[indexA][indexB] !== undefined) {
      return map[indexA][indexB]
    }
    if (indexA >= A.length || indexB >= B.length) {
      return 0
    }
    let index = -1
    // 加起来是一轮遍历
    for (let i = indexB; i < B.length; i++) {
      if (A[indexA] === B[i]) {
        index = i
        break
      }
    }
    if (index > -1) {
      map[indexA][indexB] = Math.max(
        aux(indexA + 1, index + 1) + 1,
        aux(indexA + 1, indexB),
      )
      return map[indexA][indexB]
    }
    map[indexA][indexB] = aux(indexA + 1, indexB)
    return map[indexA][indexB]
  }
  return aux(0, 0)
}