Maximum Sum BST in Binary Tree

Description

Given a binary tree root, the task is to return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

 

Example 1:

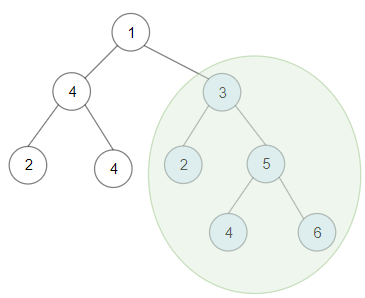
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

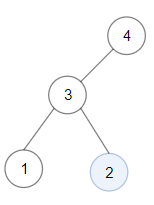
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Example 4:

Input: root = [2,1,3]
Output: 6

Example 5:

Input: root = [5,4,8,3,null,6,3]
Output: 7

 

Constraints:

• The given binary tree will have between 1 and 40000 nodes.
• Each node's value is between [-4 * 10^4 , 4 * 10^4].

Solution(javascript)

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
const maxSumBST = function (root) {
  let max = 0
  const aux = (node) => {
    if (!node) {
      return [0, true, null, null]
    }
    const [leftSum, leftValid, leftMin, leftMax] = aux(node.left)
    const [rightSum, rightValid, rightMin, rightMax] = aux(node.right)
    const sum = leftSum + rightSum + node.val
    let valid = leftValid && rightValid
    if (leftMax !== null && leftMax >= node.val) {
      valid = false
    }
    if (rightMin !== null && rightMin <= node.val) {
      valid = false
    }
    if (valid) {
      max = Math.max(max, sum)
    }
    const currentMin = leftMin === null ? node.val : leftMin
    const currentMax = rightMax === null ? node.val : rightMax
    return [sum, valid, currentMin, currentMax]
  }
  aux(root)
  return max
}