Path with Maximum Probability

Description

You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].

Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.

 

Example 1:

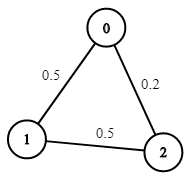
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

Example 2:

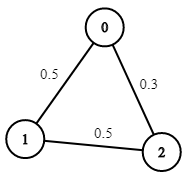
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
Output: 0.30000

Example 3:

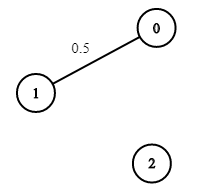
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
Output: 0.00000
Explanation: There is no path between 0 and 2.

 

Constraints:

• 2 <= n <= 10^4
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• There is at most one edge between every two nodes.

Solution(javascript)

class Heap {
  constructor(list, compare = (a, b) => a - b) {
    this.left = index => 2 * index + 1
    this.right = index => 2 * index + 2
    this.parent = index => Math.floor((index - 1) / 2)
    this.heapify = (index = 0) => {
      const { list } = this
      const leftIndex = this.left(index)
      const rightIndex = this.right(index)
      let maxIndex = index
      if (list[leftIndex] !== undefined
        && this.compare(list[maxIndex], list[leftIndex]) > 0) {
        maxIndex = leftIndex
      }
      if (list[rightIndex] !== undefined
        && this.compare(list[maxIndex], list[rightIndex]) > 0) {
        maxIndex = rightIndex
      }
      if (index !== maxIndex) {
        const temp = list[index]
        list[index] = list[maxIndex]
        list[maxIndex] = temp
        this.heapify(maxIndex)
      }
    }
    this.buildHeap = () => {
      for (let i = Math.floor(this.list.length / 2); i >= 0; i--) {
        this.heapify(i)
      }
      return this.list
    }
    this.extract = () => {
      const temp = this.list[0]
      this.list[0] = this.list[this.list.length - 1]
      this.list[this.list.length - 1] = temp
      const result = this.list.pop()
      this.heapify(0)
      return result
    }
    this.insert = (item) => {
      const { list } = this
      list.push(item)
      let index = list.length - 1
      let parentIndex = this.parent(index)
      while (list[parentIndex] !== undefined && this.compare(list[parentIndex], list[index]) > 0) {
        const temp = list[index]
        list[index] = list[parentIndex]
        list[parentIndex] = temp
        index = parentIndex
        parentIndex = this.parent(index)
      }
    }
    this.list = list
    this.compare = compare
    this.buildHeap()
  }
}


/** Similar to 787
 * @param {number} n
 * @param {number[][]} edges
 * @param {number[]} succProb
 * @param {number} start
 * @param {number} end
 * @return {number}
 */
const maxProbability = function (n, edges, succProb, start, end) {
  const adj = edges.reduce((acc, [start, end], index) => { // eslint-disable-line
    acc[start] = acc[start] || []
    acc[start].push([end, succProb[index]])
    acc[end] = acc[end] || []
    acc[end].push([start, succProb[index]])
    return acc
  }, {})
  const possibleMap = {}
  for (let i = 0; i < n; i++) {
    possibleMap[i] = 0
  }
  possibleMap[start] = 1

  const heap = new Heap([], (a, b) => b[0] - a[0])
  for (const [t, currentP] of (adj[start] || [])) {
    heap.insert([currentP, t])
  }

  while (heap.list.length > 0) {
    const [possible, from] = heap.extract()
    if (from === end) {
      return possible
    }
    for (const [t, currentP] of (adj[from] || [])) {
      const p = possible * currentP
      if (p <= possibleMap[t]) {
        continue
      }
      possibleMap[t] = p
      heap.insert([p, t])
    }
  }
  return 0
}