Interval List Intersections

Description

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.  The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval.  For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

 

Example 1:

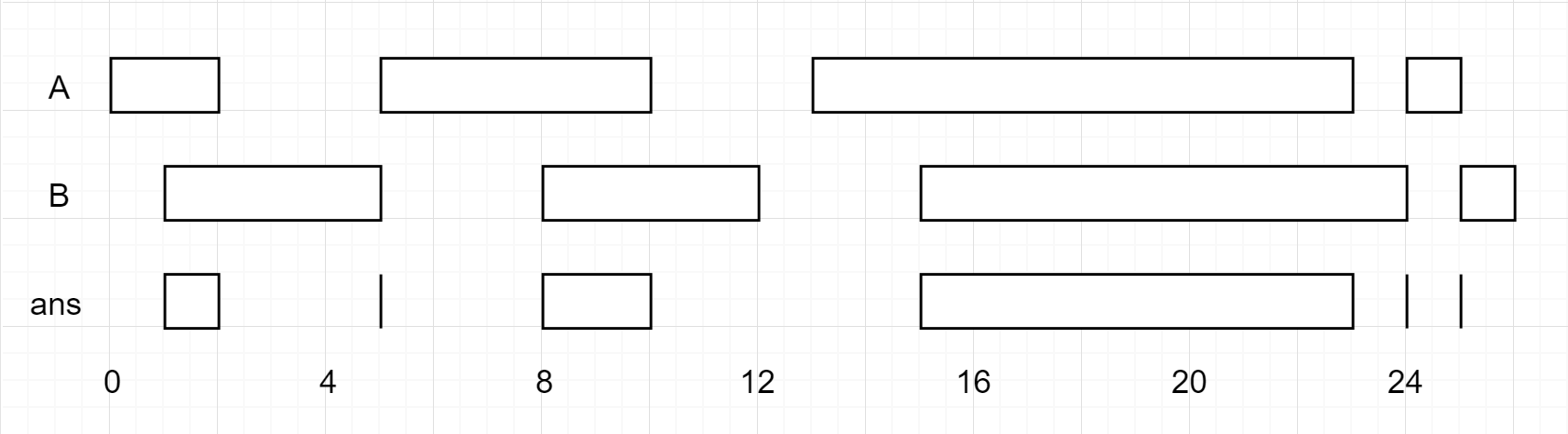
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

 

Note:

1. 0 <= A.length < 1000
2. 0 <= B.length < 1000
3. 0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9

Solution(javascript)

/**
 * @param {number[][]} A
 * @param {number[][]} B
 * @return {number[][]}
 */
const intervalIntersection = function (A, B) {
  const result = []
  let i = 0
  let j = 0
  while (i < A.length && j < B.length) {
    const [a, b] = A[i]
    const [c, d] = B[j]
    const lo = Math.max(a, c)
    const hi = Math.min(b, d)
    if (lo <= hi) {
      result.push([Math.max(a, c), Math.min(b, d)])
    }
    if (b < d) {
      i++
    } else {
      j++
    }
  }
  return result
}