Maximum Product of Splitted Binary Tree

Description

Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.

Since the answer may be too large, return it modulo 10^9 + 7.

 

Example 1:

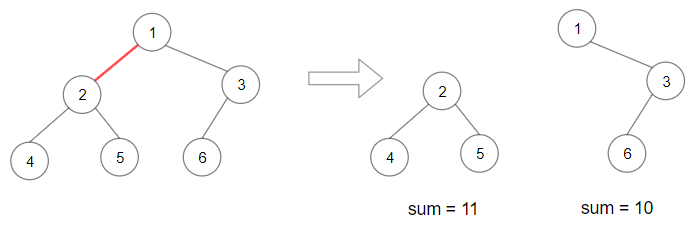
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

Example 2:

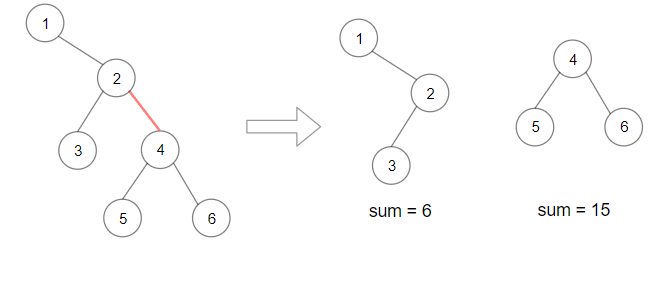
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation:  Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

Example 3:

Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025

Example 4:

Input: root = [1,1]
Output: 1

 

Constraints:

• Each tree has at most 50000 nodes and at least 2 nodes.
• Each node's value is between [1, 10000].

Solution(javascript)

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/** 1. In-order traverse + Prefix Sum(中序遍历顺序不对，行不通)
 * 2. 记录每个节点的 sum, 用根节点的 sum 减去对应的节点
 * @param {TreeNode} root
 * @return {number}
 */
const maxProduct = function (root) {
  let max = 0
  let total = 0
  const sum = (node) => {
    if (!node) {
      return 0
    }
    const leftSum = sum(node.left)
    const rightSum = sum(node.right)
    const currentSum = leftSum + rightSum + node.val
    max = Math.max(
      max, (total - leftSum) * leftSum, (total - rightSum) * rightSum,
    )
    return currentSum
  }
  total = sum(root)
  sum(root)
  return (max % (10 ** 9 + 7))
}