Parallel Courses II
Description
Given the integer n representing the number of courses at some university labeled from 1 to n, and the array dependencies where dependencies[i] = [xi, yi] represents a prerequisite relationship, that is, the course xi must be taken before the course yi. Also, you are given the integer k.
In one semester you can take at most k courses as long as you have taken all the prerequisites for the courses you are taking.
Return the minimum number of semesters to take all courses. It is guaranteed that you can take all courses in some way.
Example 1:
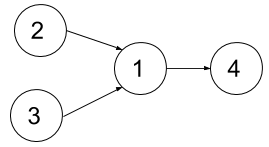
Input: n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2 Output: 3 Explanation: The figure above represents the given graph. In this case we can take courses 2 and 3 in the first semester, then take course 1 in the second semester and finally take course 4 in the third semester.
Example 2:
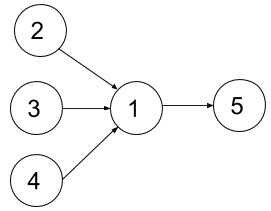
Input: n = 5, dependencies = [[2,1],[3,1],[4,1],[1,5]], k = 2 Output: 4 Explanation: The figure above represents the given graph. In this case one optimal way to take all courses is: take courses 2 and 3 in the first semester and take course 4 in the second semester, then take course 1 in the third semester and finally take course 5 in the fourth semester.
Example 3:
Input: n = 11, dependencies = [], k = 2 Output: 6
Constraints:
1 <= n <= 151 <= k <= n0 <= dependencies.length <= n * (n-1) / 2dependencies[i].length == 21 <= xi, yi <= nxi != yi- All prerequisite relationships are distinct, that is,
dependencies[i] != dependencies[j]. - The given graph is a directed acyclic graph.
Solution(javascript)
/** Greedy + topological sort
* @param {number} n
* @param {number[][]} dependencies
* @param {number} k
* @return {number}
*/
const minNumberOfSemesters = function (n, dependencies, k) {
const adjList = dependencies.reduce((acc, [a, b]) => {
acc[a] = acc[a] || []
acc[a].push(b)
return acc
}, {})
const inDegree = new Array(n + 1).fill(0)
const outDegree = new Array(n + 1).fill(0)
dependencies.forEach(([a, b]) => {
inDegree[b] += 1
outDegree[a] += 1
})
const queue = []
for (let i = 1; i <= n; i++) {
if (inDegree[i] === 0) {
queue.push(i)
}
}
let semesters = 0
while (queue.length > 0) {
const size = queue.length
queue.sort((a, b) => outDegree[b] - outDegree[a])
for (let i = 0; i < k && i < size; i++) {
const current = queue.shift()
if (current) {
(adjList[current] || []).forEach((next) => {
inDegree[next] -= 1
if (inDegree[next] === 0) {
queue.push(next)
}
})
}
}
semesters += 1
}
return semesters
}
