Minimum Possible Integer After at Most K Adjacent Swaps On Digits

Description

Given a string num representing the digits of a very large integer and an integer k.

You are allowed to swap any two adjacent digits of the integer at most k times.

Return the minimum integer you can obtain also as a string.

 

Example 1:

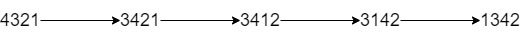
Input: num = "4321", k = 4
Output: "1342"
Explanation: The steps to obtain the minimum integer from 4321 with 4 adjacent swaps are shown.

Example 2:

Input: num = "100", k = 1
Output: "010"
Explanation: It's ok for the output to have leading zeros, but the input is guaranteed not to have any leading zeros.

Example 3:

Input: num = "36789", k = 1000
Output: "36789"
Explanation: We can keep the number without any swaps.

Example 4:

Input: num = "22", k = 22
Output: "22"

Example 5:

Input: num = "9438957234785635408", k = 23
Output: "0345989723478563548"

 

Constraints:

• 1 <= num.length <= 30000
• num contains digits only and doesn't have leading zeros.
• 1 <= k <= 10^9

Solution(javascript)

/**
 * @param {string} num
 * @param {number} k
 * @return {string}
 */
const minInteger = function (num, k) {
  const arr = num.split('').map(x => Number(x))
  const minIndex = (i, count) => {
    let index = i
    for (let j = i + 1; j < arr.length && j <= i + count; j++) {
      if (arr[j] < arr[index]) {
        index = j
      }
    }
    return index
  }
  for (let i = 0; i < arr.length; i++) {
    if (k === 0) {
      return arr.join('')
    }
    const index = minIndex(i, k)
    if (index !== i) {
      const min = arr[index]
      k -= index - i
      arr.splice(index, 1)
      arr.splice(i, 0, min)
    }
  }
  return arr.join('')
}