Longest ZigZag Path in a Binary Tree

Description

Given a binary tree root, a ZigZag path for a binary tree is defined as follow:

• Choose any node in the binary tree and a direction (right or left).
• If the current direction is right then move to the right child of the current node otherwise move to the left child.
• Change the direction from right to left or right to left.
• Repeat the second and third step until you can't move in the tree.

Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).

Return the longest ZigZag path contained in that tree.

 

Example 1:

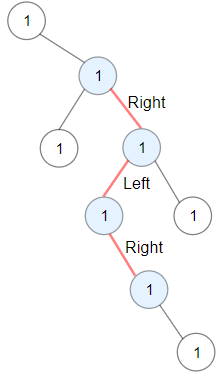
Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
Output: 3
Explanation: Longest ZigZag path in blue nodes (right -> left -> right).

Example 2:

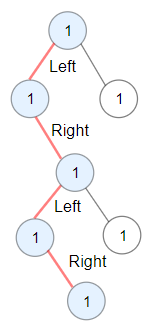
Input: root = [1,1,1,null,1,null,null,1,1,null,1]
Output: 4
Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).

Example 3:

Input: root = [1]
Output: 0

 

Constraints:

• Each tree has at most 50000 nodes..
• Each node's value is between [1, 100].

Solution(javascript)

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
const longestZigZag = function (root) {
  let max = 0
  const aux = (node) => {
    if (!node) {
      return [-1, -1]
    }
    const [,right1] = aux(node.left)
    const [left2] = aux(node.right)
    max = Math.max(
      right1 + 1,
      left2 + 1,
      max,
    )
    return [right1 + 1, left2 + 1]
  }
  aux(root)
  return max
}