Pseudo-Palindromic Paths in a Binary Tree
Description
Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.
Return the number of pseudo-palindromic paths going from the root node to leaf nodes.
Example 1:
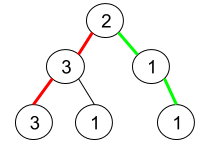
Input: root = [2,3,1,3,1,null,1] Output: 2 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 2:
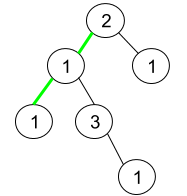
Input: root = [2,1,1,1,3,null,null,null,null,null,1] Output: 1 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 3:
Input: root = [9] Output: 1
Constraints:
- The given binary tree will have between
1and10^5nodes. - Node values are digits from
1to9.
Solution(javascript)
/**
* @param {TreeNode} root
* @return {number}
*/
const pseudoPalindromicPaths = function (root) {
let count = 0
const isValid = (arr = []) => {
let oddCount = 0
for (const v of arr) {
if (v % 2 === 1) {
oddCount += 1
}
}
return oddCount <= 1
}
const arr = new Array(10).fill(0)
const aux = (node) => {
if (!node) {
return
}
const { val } = node
arr[val] += 1
if (!node.left && !node.right) {
if (isValid(arr)) {
count += 1
}
arr[val] -= 1
return
}
aux(node.left)
aux(node.right)
arr[val] -= 1
}
aux(root)
return count
}
